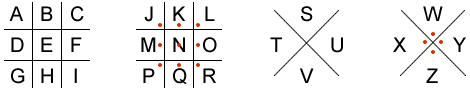Il codice “Navajo”

Tra la prima e la seconda guerra mondiale, gli USA pensarono di cifrare le loro comunicazioni semplicemente traducendole nel linguaggio degli indiani Choctaws. Pensarono insomma di sfruttare la complessità di tale linguaggio a difesa delle loro comunicazioni. Dopo l’inizio della guerra per gli USA, nel 1941, lo studio di questo genere di crittografia venne esteso e si sperimentarono i linguaggi di Commanches, Choctaws, Kiowas, Winnebagos, Seminoles, Navajos, Hopis e Cherokees. Successivamente però si optò per utilizzare esclusivamente il linguaggio Navajos.
Tra le varie tribù indiane vennero scelti proprio i Navajo perché la loro lingua appartiene a una famiglia linguistica priva di legami con qualsiasi idioma asiatico o europeo, inoltre si trattava dell’unica tribù che non fosse stata visitata da studiosi tedeschi. I “NAC”,Native American Codetalkers (parla-codice), ebbero un ruolo importantissimo nella guerra del Pacifico, contro i Giapponesi. Con il progredire della guerra nel Pacifico crebbe l’importanza dei “parla-codice” e la richiesta del loro aiuto aumentò rapidamente. Non tutti i marines però erano al corrente della presenza dei navajo e i “parla-codice” venivano a volte scambiati per soldati nemici, catturati dagli americani e rilasciati soltanto dopo l’intervento di soldati del loro stesso reparto. Per evitare questo genere di incidenti ad ogni navajo venne affiancato un marine che aveva il compito di proteggere non solo lui ma, soprattutto, il codice. Il “parla-codice” non doveva essere catturato dai giapponesi, perché avrebbe potuto rivelare la chiave del codice, e il marine aveva ricevuto l’ordine di ucciderlo prima che cadesse prigioniero.
Inizialmente si presentarono alcuni problemi dovuti al fatto che i navajo non avevano nel loro idioma i moderni termini tecnici e militari. Uno scoglio che venne facilmente superato inventando nomi di fantasia. Ad esempio si decise di usare nomi di uccelli per gli aerei e di pesci per le navi da guerra. In tal modo il cacciabombardiere era lo sparviero (Gini, in codice navajo), l’aereo spia era il gufo (Ne-as-jah).
Il loro codice è uno dei più sicuri e dei più semplici, uno dei pochi rimasto inviolato, ma il ruolo dei navajo nella seconda Guerra mondiale rimase un segreto militare fino al 1968, quando vennero finalmente autorizzati a rendere pubblico il loro contributo alla guerra. L’attività dei codetalkers viene ricordata nel film Windtalker, diretto dal regista cinese Yusen Wu.

Il cifrario di Cesare

Si narra che Giulio Cesare usava per le sue corrispondenze riservate un codice di sostituzione molto semplice, nel quale la lettera chiara veniva sostituita dalla lettera che la segue di tre posti nell’alfabeto: la lettera A è sostituita dalla D, la B dalla E e così via fino alle ultime lettere che sono cifrate con le prime come nella tabella che segue (che fa riferimento all’odierno alfabeto internazionale).

Chiaro a b c d e f g h i j k l m n o p q r s t u v w x y z

Cifrato D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Prendendo come esempio la frase Servono rinforzi si otterrà il seguente messaggio:

Chiaro servonorinforzi

Cifrato VHUYRQRULQIRUCL

Più in generale si dice codice di Cesare un codice nel quale la lettera del messaggio chiaro viene spostata di un numero fisso di posti, non necessariamente tre.

Poiché l’alfabeto internazionale è composto da 26 caratteri sono possibili 26 codici di Cesare diversi dei quali uno (quello che comporta uno spostamento di zero posizioni) darà un cifrato uguale al messaggio chiaro iniziale. Non è certo un sistema sofisticato, ma risultò estremamente utile al suo ideatore : era cioè funzionale perché all’epoca in cui venne usato presentava una capacità di resistenza agli attacchi (tentativi di decifratura) proporzionata all’importanza dei messaggi ed alle capacità tecniche degli assalitori.

Prova tu stesso il cifrario di Cesare

Prova tu stesso a cifrare un messaggio segreto con il codice di Cesare; inserisci il messaggio nella finestrella accanto a “Chiaro”, specifica il numero di caratteri da spostare, quindi fai click su “Cifra” (eventuali lettere minuscole sono convertite in maiuscolo, spazi e segni di interpunzione sono ignorati).

Inizio modulo

Chiaro Spostamento Cifrato

Se invece volete provare a decifrare un testo cifrato con questo tipo di schema, è possibile procedere semplicemente tenendo a mente che stiamo lavorando su un anello chiuso composto da 26 lettere. Al termine delle 26 lettere si riparte da capo. Quindi, se la lettera “A”, spostata di 4 posti, viene tradotta in “E”, allora la lettera “E”, spostata di 26-4=22 posti, sarà nuovamente tradotta in “A”. Lo stesso vale per tutte le lettere. Se si cifra effettuando un offset di x caratteri, si deve decifrare con un offset di 26-x caratteri.

Fine modulo

Pigpen

Il cifrario Pigpen (recinto per maiali) veniva utilizzato nel Settecento, dai massoni, per evitare che le proprie comunicazioni venissero intercettate. Attualmente viene utilizzato per gioco, dagli scolari. Si tratta di una semplicissima sostituzione delle lettere con dei simboli, secondo il seguente schema:

Seguendo tale schema risulterebbe:

a =

b =

……

z =

Dunque secondo tale schema, il codice : andrebbe tradotto semplicemente come “ciao”.

Se è nota la chiave di cifratura del pigpen, allora è semplicissimo decifrarlo. Altrimenti non risulta particolarmente difficile ricavare la chiave giusta, magari con analisi di frequenze.

Il cifrario Atbash

Il libro di Geremia nella Bibbia usa un semplicissimo codice monoalfabetico per cifrare la parola Babele; la prima lettera dell’alfabeto ebraico (Aleph) viene cifrata con l’ultima (Taw), la seconda (Beth) viene cifrata con la penultima (Shin) e così via; da queste quattro lettere è derivato il nome di Atbash (A con T, B con SH) per questo codice. Usando il moderno alfabeto internazionale, l’Atbash può essere riassunto con la seguente tabella di cifratura:

CHIARO a b c d e f g h i j k l m

CIFRATO Z Y X W V U T S R Q P O N

CHIARO n o p q r s t u v w x y z

CIFRATO M L K J I H G F E D C B A

La traduzione della parola soccorso diventerebbe HLXXLIHL

Il codice Atbash è quindi simile ma meno complesso di quello di Cesare, poichè al contrario di quest’ultimo prevede solo una possibile sostituzione.

Il disco cifrante di L.B.Alberti

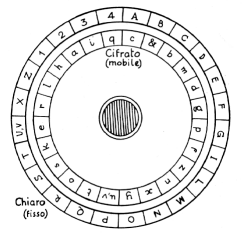
Leon Battista Alberti, nel suo Trattato della cifra, ha proposto un disco composto di due cerchi cifranti concentrici: uno esterno fisso con 24 caselle contenenti 20 lettere latine maiuscole (inclusa la Z, con U=V ed escluse H J K W Y) ed i numeri 1 2 3 4 per il testo chiaro; ed uno interno mobile, con le 24 lettere latine minuscole per il testo cifrato. Le 20 lettere maiuscole messe in ordine alfabetico; le 24 minuscole in disordine (questa è una norma fondamentale, trascurata da molti successori dell’Alberti, senza la quale si ha una semplice generalizzazione del codice di Cesare).

Fissata una lettera maiuscola come indice (ad es. B) si deve spostare il disco mobile interno e scrivere, come prima lettera del crittogramma, la lettera minuscola che corrisponde alla B; quindi cifrare alcune parole con la lista risultante. Quando si decide di cambiare la lista cifrante si scriverà la nuova lettera chiave in maiuscolo in modo da indicare chiaramente al corrispondente il cambio di lista. Ciò fatto, si porterà quella lettera ad affacciare l’indice B ed in questa nuova posizione si cifreranno altre parole secondo la nuova lista.

Per aumentare la segretezza (le lettere maiuscole costituiscono un aiuto non solo per il corrispondente ma anche per il “nemico”) l’Alberti suggerisce di usare uno dei quattro numeri per segnalare il cambio di alfabeto; la lettera minuscola corrispondente al numero sarà la nuova chiave; non vi sono quindi più lettere maiuscole e la cifra risulta così molto più sicura, e decisamente superiore a quelle che la seguirono nel tempo, e in particolare alla fin troppo famosa Tavola di Vigénère.

Si tratta in definitiva di una delle cifre polialfabetiche più sicure, che non ottenne il successo meritato anche per la decisione dell’Alberti di tenerla segreta (il suo trattato fu pubblicato solo un secolo più tardi a Venezia insieme ad altri suoi “opuscoli morali” e passò quasi inosservato).

Vigenere

Il codice di Vigenere, ideato da Blaise De Vigenere nel 1586, può essere considerato un caso particolare del sistema Vernam (che fu ideato da G.S.Vernam nel 1926). Si tratta di un codice a sostituzione polialfabetica, che può essere attaccato col metodo Kasiski. Da un lato il sistema Vigenere può considerarsi un’estensione del codice di Cesare, dove invece di shiftare tutte le lettere di una stessa quantità si effettua l’offset in base alla chiave. In altre parole si effettua la somma dei valori numerici corrispondenti alle lettere del testo in chiaro e a quelle della chiave, per esempio assegnando i numeri (a partire dallo zero) alle lettere alfabeticamente ordinate. Ecco un esempio:

Chiave: FULMINE

Messaggio in chiaro: TANTISALUTIATUTTI

Messaggio cifrato: YUYFQFEQOEUIGYYNT

Alla lettera F della chiave corrisponde il numero 5 (a=0, b=1, ….f=5, …..). Alla lettera T del messaggio corrisponde il numero 20. La somma dei due numeri è 25, a cui corrisponde la lettera y. Si procede allo stesso modo per le altre lettere, riprendendo la chiave dall’inizio se dovesse risultare più corta del testo in chiaro.
Da un altro punto di vista, il codice di Vigenere può essere considerato una restrizione, un caso particolare del sistema Vernam. Mentre il Vernam impone che la lunghezza della chiave sia almeno pari a quella del testo in chiaro, nel Vigenere la chiave è più corta del testo da cifrare e quindi deve essere ripetuta. E questo è proprio il tallone d’Achille del Vigenere, perchè lo rende vulnerabile ad attacchi crittoanalitici di vario genere. Il Vernam è invece un algoritmo perfetto, inviolabile, sempre che la chiave sia generata in modo casuale.

Per velocizzare le operazioni di cifratura-decifratura, Vigenere introdusse una semplice tavola costituita da righe di lettere alfabeticamente ordinate, shiftate di 1 posto riga per riga:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z B C D E F G H I J K L M N O P Q R S T U V W X Y Z A C D E F G H I J K L M N O P Q R S T U V W X Y Z A B D E F G H I J K L M N O P Q R S T U V W X Y Z A B C E F G H I J K L M N O P Q R S T U V W X Y Z A B C D F G H I J K L M N O P Q R S T U V W X Y Z A B C D E G H I J K L M N O P Q R S T U V W X Y Z A B C D E F H I J K L M N O P Q R S T U V W X Y Z A B C D E F G I J K L M N O P Q R S T U V W X Y Z A B C D E F G H J K L M N O P Q R S T U V W X Y Z A B C D E F G H I K L M N O P Q R S T U V W X Y Z A B C D E F G H I J L M N O P Q R S T U V W X Y Z A B C D E F G H I J K M N O P Q R S T U V W X Y Z A B C D E F G H I J K L N O P Q R S T U V W X Y Z A B C D E F G H I J K L M O P Q R S T U V W X Y Z A B C D E F G H I J K L M N P Q R S T U V W X Y Z A B C D E F G H I J K L M N O Q R S T U V W X Y Z A B C D E F G H I J K L M N O P R S T U V W X Y Z A B C D E F G H I J K L M N O P S S T U V W X Y Z A B C D E F G H I J K L M N O P Q R T U V W X Y Z A B C D E F G H I J K L M N O P Q R S U V W X Y Z A B C D E F G H I J K L M N O P Q R S T V W X Y Z A B C D E F G H I J K L M N O P Q R S T U W X Y Z A B C D E F G H I J K L M N O P Q R S T U V X Y Z A B C D E F G H I J K L M N O P Q R S T U V W Y Z A B C D E F G H I J K L M N O P Q R S T U V W X Z A B C D E F G H I J K L M N O P Q R S T U V W X Y

Supponendo di voler cifrare (vedi esempio sopra) la lettera T, con la chiave F. L’elemento cifrato è quello appartenente alla colonna che inizia per T ed alla riga che inizia per F. Otteniamo così l’elemento y. E’possibile testare in modo automatico questo tipo di crittografia utilizzando il modulo sottostante. Si tratta di un semplice esempio che elabora solo le 26 lettere dell’alfabeto, senza far distinzione tra maiuscole e minuscole. Nel caso in cui la chiave dovesse essere lunga quanto il testo da cifrare, allora state passando dal Vigenere al Vernam.

Inizio modulo

Vigenere Chiave: Messaggio in chiaro: Messaggio cifrato:

Fine modulo

Vernam

Il sistema Vernam è un caso particolare della cifratura One time-Pad. La cifratura detta a chiave infinita o one-time pad consiste nel generare una chiave composta il più possibile da lettere, numeri e simboli disposti in modo casuale, e di una lunghezza almeno pari alla lunghezza del testo da criptare. Quindi per ogni carattere del testo in chiaro aggiungiamo (come somma di valori ASCII ad esempio) un carattere della chiave, ottenendo il testo criptato. E’ facile intuire che una cosa del genere è praticamente impossibile da decifrare, in quanto si basa su una chiave ottenuta in modo assolutamente casuale (entropia massima) e senza la possibilità di analizzare delle ripetizioni nel testo, in quanto la chiave ha appunto la lunghezza stessa del testo. Questo sistema di codifica è usato per ottenere i più alti gradi di sicurezza militare, ma ha il grosso difetto di non essere impiegabile su vasta scala o per messaggi particolarmente lunghi. Alcuni algoritmi sono stati costruiti approssimando il sistema a chiave infinita con l’espansione di una chiave relativamente breve. Il sistema “Vernam”, ad esempio, usato nelle trasmissioni telegrafiche, usava lunghi nastri di carta contenenti dei bit casuali, i quali erano aggiunti ai bit del messaggio originario.
Il sistema Vernam può comportare degli svantaggi dovuti all’espansione della chiave, se questa ha lunghezza molto inferiore a quella del messaggio da cifrare. Risulta dunque conveniente usare chiavi molto lunghe e, soprattutto, più casuali possibili. Si tratta di un algoritmo efficientissimo, ma, essendo a chiave privata, comporta non pochi limiti.
Tonycrypt.com ha realizzato un programma che consente di cifrare secondo il sistema Vernam. Il programma può essere scaricato

Alain Turing e la macchina Enigma

Durante la seconda guerra mondiale tutte le comunicazioni militari tedesche venivano criptate con una macchina di cifra chiamata Enigma, ideata dall’ingegnere tedesco Arthur Scherbius. Questa macchina è una rappresentante niente affatto indegna di una classe di cifrari a rotore, utilizzati fino all’introduzione di cifrari elettronici e microelettronici che hanno sconvolto e trasformato il mondo della crittografia. Per forzare l’Enigma (alcuni dettagli della soluzione sono tenuti segreti fino ad oggi) Turing, per conto del governo inglese, si servì di gigantesche macchine chiamate appunto Colossi, che possono considerarsi i precursori dei moderni calcolatori elettronici. Turing è autore di ricerche estremamente raffinate e molto profonde sul concetto logico-matematico di calcolabilità: la strumento che egli ha proposto per affrontare il problema è noto oggi col nome di macchina di Turing. Le macchine di Touring non hanno niente da spartire coi Colossi, non possiedono né valvole, né transistor, né circuiti integrati(come i calcolatori della prima, della seconda o della terza generazione), esse sono macchine “astratte” e meramente “ideali” che esistono solo mente di Turing e in quelle dei logici che proseguono le sue ricerche.
Per rendersi conto di quanto i tempi siano cambiati basterà ricordare che l’Enigma aveva un grande inconveniente: era sprovvisto di stampante. I risultati apparivano illuminati su una tastiera apposita, lettera dopo lettera, e una persona doveva provvedere a trascriverli a mano su un foglio di carta. Una stampante elettro-meccanica avrebbe appesantito troppo il congegno e lo avrebbe reso poco maneggevole: un problema che la tecnica odierna consente di superare senza difficoltà.

Il cifrario RSA

L’RSA è un cifrario a chiave pubblica che permette di cifrare un messaggio attraverso un procedimento che sfrutta le proprietà dei numeri primi.

In termini molto semplici: fissati due numeri h ed n, che costituiscono la chiave pubblica, si considera un terzo numero d che costituisce la chiave privata (i dettagli sul calcolo di questi parametri sono esposti più giù). Sia m il messaggio da cifrare. L’operazione da compiere è la seguente:

c=m^h mod n.

La chiave di decifrazione è costituita dal numero intero d, segreto, che permette di recuperare m grazie alla formula:

m=c^d mod n.

L’RSA viene considerato oggi uno dei sistemi di crittografia più sicuri perchè, essendo violabile solo mediante attacchi di forza bruta, la rottura del codice richiederebbe tempi e risorse economiche elevatissimi. Ma i supercomputer di cui dispongono i grandi governi e le continue ricerche matematiche non ci garantiscono, chiaramente, la massima sicurezza.

Esporrò adesso, in termini più tecnici, i principi di funzionamento dell’RSA.

• Si determini la prima chiave n, prodotto di p e q, due numeri primi molto elevati, tali che la fattorizzazione di n sia estremamente difficile;
• Si calcoli dunque il valore della funzione di Eulero di n: b=phi(n)=(p-1)*(q-1) il cui valore rimane segreto; si scelga ancora un intero d tale che d e phi(n) siano primi tra loro (d non risulterà necessariamente primo, ma deve essere minore di phi(n)). Infine si trovi h che è il più piccolo x (intero) per cui (dx-1)/phi(n) é un numero intero.

In questo modo abbiamo determinato i numeri n, h e d di cui abbiamo già parlato.

Se chiamo k la quantità (dx-1)/phi(n), ottengo dx=dh=kphi(n)+1. Posso allora dimostrare perchè m=c^d mod n:

Il codice RSA viene considerato sicuro perchè, essendo la formula di decifrazione basata su phi(n) calcolabile solo se a conoscenza di p e q, non esiste (o perlomeno non è noto) un algoritmo per scomporre n nei suoi fattori primi p e q in tempi accettabili. Bisognerebbe effettuare attacchi di forza bruta, provando cioè tutti i possibili casi. Fattorizzare un numero di 664 bit richiede almeno 10²³ passi usando gli algoritmi più efficienti; per cui ipotizzando di avere una rete costituita da un milione di computer con ciascuno di loro che esegue un milione di passi al secondo, il tempo impiegato per fattorizzare n sarebbe dell’ordine dei 4000 anni. Se poi n fosse un numero a 1024 bit la stessa rete impiegherebbe 10¹⁰ anni per fattorizzarlo . Potrebbe sorgere il dubbio che esista un modo di calcolare phi(n) senza passare per p e q: questa ipotesi in effetti è verificabile ed è uno dei tanti motivi per non dare massima fiducia a questo algoritmo di cifratura.

Esempio

 n=p*q=5*7=35

 b=phi(35)=(5-1)(7-1)=24

 d=7 (primo con 24)

 k=(7x-1)/24       da cui:   x=(k*24+1)/7

 Fisso k=2 in modo da ottenere un numero x intero. Quindi k=2 e x=h=7.

Ho trovato tutti i parametri che mi servivano e, a questo punto, suppongo che il messaggio da cifrare sia m=3. Procedo e calcolo:

c=m^h mod n=3⁷mod 35=2187 mod 35=17

Se adesso volessi decifrare il messaggio, essendo a conoscenza della chiave segreta d, procedo in questo modo:

m=c^d mod n=17⁷mod 35=3

Elevazione a potenza modulare

L’operazione dell’elevazione a potenza modulare consiste nel calcolare x^y mod z dove x, y e z sono interi. Ma, lavorando con numeri estremamente grandi, gli elaboratori non sono in grado di eseguire da soli questi calcoli. E’allora necessario fare uso di algoritmi di calcolo che, benchè laboriosi, ci consentono di raggiungere il nostro scopo. Al momento, per la realizzazione del mio programma di crittografia a chiave pubblica basato sull’RSA, sto utilizzando il metodo naive, sotto illustrato. Ma ritenendolo poco efficiente (richiede un enorme lavoro della CPU) penso che lo sostituirò con un altro più veloce.

Metodo naive

Si può schematizzare questo metodo con il seguente algoritmo:

a=1
for i=1 to y do
a=(a*x)mod z
next

In pratica si calcola a=(a*x)mod z ripetendo l’operazione y volte. A questo punto il valore finale di a sarà il risultato di x^y mod z, che abbiamo ottenuto evitando di lavorare con numeri troppo grandi. Tale algoritmo non è comunque molto efficiente, essendo il numero di cicli da eseguire uguale ad y. I metodi realmente utilizzati sono 2: il metodo “Left to right” e il metodo “Right to left”. Ma parlerò in seguito di questi algoritmi, essendo ancora miei attuali argomenti di studio.

Attacchi RSA

Osserviamo che per un crittoanalista rompere l’RSA equivale a calcolare (n). Infatti, se n e (n) sono conosciuti ed n è il prodotto di due primi p e q, n può essere facilmente fattorizzato risolvendo il seguente sistema di 2 equazioni in 2 incognite: n = p q e (n)= (p – 1)(q – 1). Nelle due incognite p e q. Sostituendo q = n / p nella seconda equazione se ne ottiene un’unica di secondo grado nella sola incognita p:

p² – (n – (n) + 1)p + n = 0.

Le due radici di questa equazione sono i fattori p e q. Quindi se un crittoanalista conosce il valore di (n) può fattorizzare n e rompere il sistema.

Esempio Supponiamo che il crittoanalista conosca (n) = 84754668 e n = 84773093.Queste informazioni gli permettono di scrivere l’equazione: p² – 18426p + 84773093 = 0. Risolvendo l’equazione si ottengono le due radici 9539 e 8887 che rappresentano i fattori p e q di n.

Blowfish

Blowfish è un cifrario a blocchi sviluppato da Bruce Schneier, autore del famoso libro Applied Cryptography. Blowfish opera su blocchi di 64 bits con chiavi di lunghezza variabile fino a 448 bits. Questo algoritmo utilizza varie tecniche tra le quali la rete Feistel, le S-box dipendenti da chiavi e funzioni non invertibili che lo rendono, forse, l’algoritmo più sicuro attualmente disponibile. Non si conoscono al momento attacchi nei suoi confronti.

Il cifrario DES

DES sta per Data Encryption Standard ed e’ un cifratore a blocco iterativo sviluppato alla IBM e definito dal governo degli Stati Uniti come standard ufficiale nel 1977. La dimensione dei blocchi DES e’ di 64 bit, ed usa una chiave a 56 bit (16 cicli) durante la cifratura (gli altri 8 bit servono per la correzione degli errori). Questo algoritmo è stato violato soltanto grazie all’enorme potenza di calcolo dei moderni elaboratori. Il 17 luglio 1998, l’EFF (Electronic Frontier Foundation) ha realizzato una scheda multiprocessore in grado di violare un sistema DES a 64 bit in meno di tre giorni, generando tutte le 2^56 chiavi possibili. Questa scheda è basata sull’utilizzo di alcuni chip chiamati “Deep Crack”, estremamente veloci perchè presentano tutte le operazioni da eseguire già implementate sull’hardware.

Crittoanalisi

Analisi delle frequenze

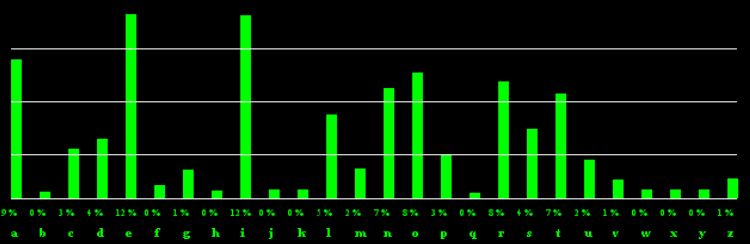
Nel caso dei cifrari monoalfabetici, ad ogni lettera se ne sostituisce un’altra secondo opportune regole. Se ad esempio sostituissimo la c con la x, la i con la y, poi a=r e o=b, potremmo scrivere la parola “ciao” come “xyrb”. Sembra trattarsi di un sistema di crittografia estremamente sicuro e, in primo luogo, piuttosto difficile da violare. In realtà è molto facile attaccarlo e violarlo: basta conoscere le proprietà statistiche del linguaggio con cui il testo è stato scritto. In questo modo non bisogna fare molta fatica per rivelare esattamente tutto il contenuto reale del crittogramma. Tonycrypt ha creato un programma che consente di effettuare automaticamente e rapidamente l’analisi delle frequenze di un testo. Si tratta di un programma gratuito disponibile nella sezione download o scaricabile cliccando qui. Per realizzare lo schema delle frequenze con cui si presentano le lettere della lingua italiana, abbiamo pensato di analizzare un testo sufficientemente lungo: la Convenzione di Ginevra relativa al trattamento dei prigionieri di guerra. Ecco dunque uno schema della ricorrenza delle lettere della lingua italiana:

Ecco i valori non approssimati (nel grafico dobbiamo tener conto anche dell’estetica, dunque riportiamo solo i valori interi) delle frequenze letterarie in lingua italiana: Lettera a: 9,651 %; Lettera b: 0,481 %; Lettera c: 3,469 %; Lettera d: 4,142 %; Lettera e: 12,791 %; Lettera f: 0,929 %; Lettera g: 1,9984 %; Lettera h: 0,517 %; Lettera i: 12,730 %; Lettera j: 1,584E-03 %; Lettera k: 7,921E-04 %; Lettera l: 5,809 %; Lettera m: 2,031 %; Lettera n: 7,690 %; Lettera o: 8,760 %; Lettera p: 3,018 %; Lettera q: 0,350 %; Lettera r: 8,140 %; Lettera s: 4,835 %; Lettera t: 7,290 %; Lettera u: 2,685 %; Lettera v: 1,283 %; Lettera w: 0 %; Lettera x: 0 %; Lettera y: 0 %; Lettera z: 1,387 %;

Supponiamo adesso di trovarci davanti ad un testo cifrato in cui si è deciso di sostituire la a con la x, la e con la y e così via. E supponiamo che il testo originale, in chiaro, fosse scritto in italiano. Sottoponiamo tale testo ad un’analisi delle frequenze. Troveremo che la x presenta una ricorrenza vicina al 9%, la y intorno al 12% e così via. Confrontando tali risultati con la soprastante tabella delle ricorrenze tipiche della lingua italiana, immediatamente ci si accorge della sostituzione effettuata.

Vediamo un esempio pratico di quanto appena esposto: supponiamo di trovarci davanti al seguente testo:

YHUVRODPHWDGHJOLDQQLXQILVLFRLQJOHVHGDYLGGHXWVFKGXUDQWHXQDFRQIHUHQCD VXOODILVLFDTXDQWLVWLFDHEEHOLGHDGLFUHDUHXQFDOFRODWRUHTXDQWLVWLFRTXHV WDHXQDLGHDULYROXCLRQDULDLQTXDQWRLFDOFRODWRULWUDGLCLRQDOLVLFRPSRUWDQ RVHFRQGROHOHJJLGHOODILVLFDFODVVLFDHTXLQGLFRQOHOLPLWDCLRQLFKHQRLWXWW LFRQRVFLDPRPDXQFDOFRODWRUHTXDQWLVWLFRDYUHEEHXQDSRWHQCDGLFDOFRORWHRU LFDPHQWHLQILQLWDWDOHGDSRWHULQYHUWLUHXQDOJRULWPRDIDWWRULCCDCLRQHFRPH OUVDSUHVVRFKHLVWDQWDQHDPHQWHUHQGHQGRTXLQGLDVVROXWDPHQWHLQXWLOLLVLVW HPLGLFULWWRJUDILDDOJRULWPLFDODVSLHJDCLRQHGHOIXQCLRQDPHQWRGLXQFDOFRO DWRUHTXDQWLVWLFRHFRVDDVVDLFRPSOHVVDHQRQHGHWWRFKHVLSRVVDUHDOLCCDUHLQ SUDWLFDDOPHQRLQWHPSLEUHYLDQFKHVHVLVRVSHWWDFKHJOLXVDQHDEELDQRJLUHDOL CCDWRHVHPSODULPDDQFKHVROROLSRWHVLGLXQDVXDIXWXUDUHDOLCCDCLRQHSRQHGHL VHULLQWHUURJDWLYLVXOOXWLOLCCRGHOODFULWWRJUDILDDOJRULWPLFDVSHFLDOPHQ WHSHUTXHLGRFXPHQWLFKHGHYRQRULPDQHUHULVHUYDWLSHUXQSHULRGRGLWHPSRDEED VWDQCDOXQJRTXLQGLDOODOXFHGLTXHVWRIDWWRVLLPSRQHXQUDGLFDOHFDPELDPHQWR GLVWUDWHJLDQHOODFULWWRJUDILDDWWXDOHQRQEDVWDSLXDXPHQWDUHODOXQJKHCCDG HOOHFKLDYLSHUUHQGHUHVLFXURXQGRFXPHQWRSHULSURVVLPLDQQLVHPSUHQHOOLSRW HVLGLDYYHQWRGHOFDOFRODWRUHTXDQWLVWLFRPDELVRJQDULFRUUHUHDTXDOFRVDGLF RPSOHWDPHQWHQXRYR

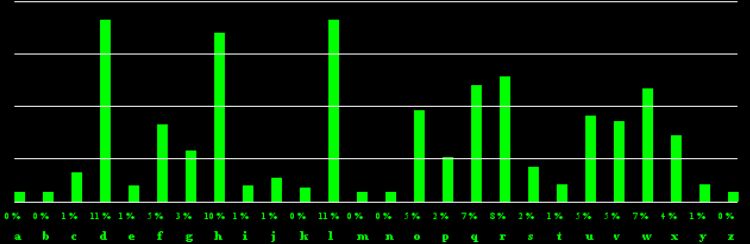
Effettuiamo un’analisi di frequenze di tale testo mediante il programma Frequency che ho sviluppato per Tonycrypt:

A questo punto non è necessaria grande intelligenza per capire cosa sta succedendo. Tutto l’andamento delle frequenze risulta traslato di 3 lettere. Chi ha cifrato il testo si è limitato ad effettuare un offset di 3 posti, utilizzando il codice di Cesare. La lettera d presenta una frequenza di 11 %, confrontabile, nella tabella della lingua italiana, a quella della a=9 %. Nel testo cifrato h=10 % mentre in lingua italiana e=12 %. Nel testo cifrato l=11 % mentre in lingua italiana i=12 %. E così via: tutto il testo originale è stato sottoposto ad un offset di 3 posti. A questo punto non ci resta che procedere inversamente. Decifriamo applicando il codice di Cesare al contrario, cioè con un offset di 26-3=23 posti (potete provare voi stessi dalla pagina dedicata al codice di Cesare). Risultato:

VERSOLAMETADEGLIANNIUNFISICOINGLESEDAVIDDEUTSCHDURANTEUNACONFERENZASULLAFIS ICAQUANTISTICAEBBELIDEADICREAREUNCALCOLATOREQUANTISTICOQUESTAEUNAIDEARIVOLU ZIONARIAINQUANTOICALCOLATORITRADIZIONALISICOMPORTANOSECONDOLELEGGIDELLAFISI CACLASSICAEQUINDICONLELIMITAZIONICHENOITUTTICONOSCIAMOMAUNCALCOLATOREQUANTI STICOAVREBBEUNAPOTENZADICALCOLOTEORICAMENTEINFINITATALEDAPOTERINVERTIREUNAL GORITMOAFATTORIZZAZIONECOMELRSAPRESSOCHEISTANTANEAMENTERENDENDOQUINDIASSOLU TAMENTEINUTILIISISTEMIDICRITTOGRAFIAALGORITMICALASPIEGAZIONEDELFUNZIONAMENT ODIUNCALCOLATOREQUANTISTICOECOSAASSAICOMPLESSAENONEDETTOCHESIPOSSAREALIZZAR EINPRATICAALMENOINTEMPIBREVIANCHESESISOSPETTACHEGLIUSANEABBIANOGIREALIZZATO ESEMPLARIMAANCHESOLOLIPOTESIDIUNASUAFUTURAREALIZZAZIONEPONEDEISERIINTERROGA TIVISULLUTILIZZODELLACRITTOGRAFIAALGORITMICASPECIALMENTEPERQUEIDOCUMENTICHE DEVONORIMANERERISERVATIPERUNPERIODODITEMPOABBASTANZALUNGOQUINDIALLALUCEDIQU ESTOFATTOSIIMPONEUNRADICALECAMBIAMENTODISTRATEGIANELLACRITTOGRAFIAATTUALENO NBASTAPIUAUMENTARELALUNGHEZZADELLECHIAVIPERRENDERESICUROUNDOCUMENTOPERIPROS SIMIANNISEMPRENELLIPOTESIDIAVVENTODELCALCOLATOREQUANTISTICOMABISOGNARICORRE REAQUALCOSADICOMPLETAMENTENUOVO

Naturalmente il sistema di analisi delle frequenze è applicabile al caso più generale in cui ad ogni lettera se ne sostituisce arbitrariamente un’altra, senza nessun tipo di regola. Il caso appena citato, dell’algoritmo di Cesare, è solo un esempio particolare di sostituzione monoalfabetica. Il programma Frequency è gratuito